手写 Attention 注意力机制及理解

背景问题

RNN 和各种变体 RNN 中 LSTM/GRU 都存在一个问题，就是如何解决长距离信息的感知。RNN 的解决办法是加大 sequence，更长的窗口记得更加久远的信息；LSTM 和 GRU 就是把记忆设置成不同的权重，对重要的信息加大权重。Attention 又是另外一个角度，去解决这个问题。

Attention 是什么

Attention 中文是注意力机制，是对某个事物的某部分的关注点。

从人脑的角度想，时间和资源都是有限的，所以只能在一定的限度内去关注某些部分。比如看到一群人的照片，我们自然去找美女；看一个美女的照片，我们自然去看美女的眼睛。我们为什么会不自主的去看这些部分而不是看全景呢？因为我们的注意力资源是有限的，我们只对关注点高的部分感兴趣。
这是属于在我们人脑里面的注意力机制。
从模型的角度想，用数学将他们建模，他们应该是注意力得分最高的部分，也就是模型可以重点关注的地方。

总结，上述就是 Attention Score 的基本的理解。谁得分高，谁就可以得到更加多的关注。

下面把 Attention Score 用在一段话的理解上。

我们使用一句话作为例子：姚明，他爸有 2 米高，他从小的数学成绩并不好，经常旷课，他爱吃苹果，他血型是 A。爱玩游戏，他最喜欢的游戏就是塞尔达传说，他还经常逃课去玩；有时候他会打一下篮球和兵乓球，他最喜欢的运动是跑步。他现在身高是 2.13 米，体重是 200 斤，鞋子要穿 48 码的。
请问：他为什么可以长这么高。

从人脑的角度，“姚明为什么这么高”，很自然的想到，他父母高，基因好。之所以有这个判断，是因为问题，和 “父母高”这个信息是 关联度最高的。
从模型的角度想，用数学将他们建模，即问题和 信息的某个部分 ，计算的Score 得分最高，所以他们的关联度最高，即他们具有逻辑相关性。

总结，Attention 机制 在自然语言理解上，即相互的 Score 越高分，即相互的关联性就越大，即他们具有逻辑性。

题外话：这个有点像逻辑。
我们大脑是神经元构成的。神经元，即是给一个高电平就是 1 ，给一个低电平就是 0 的触角；这个触角，又可以触发另外的神经元。这种就是 “一生二，二生三，三生万物”的体现。因为这种触角的触发，就在我们的大脑里面形成了逻辑。
Attention Score，有可能构成了模型领域中的 _基础触角_，最后形成了模型领域中逻辑。

分概念讲解

从上面的例子可以简单的梳理出 Attention 机制。但是落到细节里面，Attention Score 怎么计算，就是从实际的数学模型的角度去说明了。下面就 Attention Score 怎么去计算为线头，来讲解不同概念。

下面是一步一步的说明 Attention 机制的各种组件，和他们能够解决到什么问题。

QKV 机制

Query Key Value

如果对上述的那句话分成不同的片段：“他爸有 2 米高” seg1，“他从小的数学成绩并不好” seg2，“经常旷课” seg3，“他爱吃苹果” seg4，“他血型是 A” seg5，每个片段都携带了一定量的信息，我们统称他们携带的信息是 隐状态 hidden。对应着，片段的隐状态就是 h1, h2…h5。

面对 “姚明为什么这么高” 问题的时候，自然的就认为 seg1 的关联性是最高的。但是如果面对 “他三角函数不懂”问题的时候，显然是 seg2 的关联性是最高的。
所以的出，同一个query 对应不同的 segment 的，有不同的 Attention Score；不同的 query 都应该对同一批的 segment 有不同的 Attention Score。

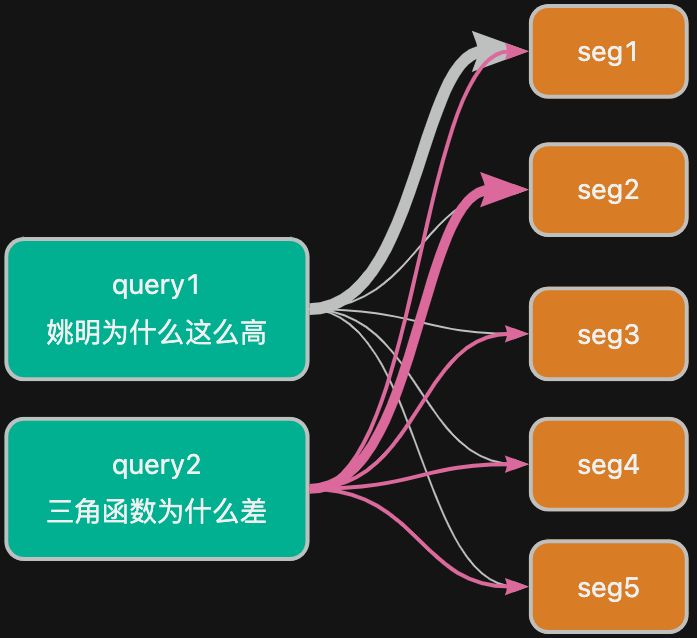
如上图所示，就是连线的宽度不同，显示了 query 和不同 segment 之间的相关性，即不同的得分。

如果基于传统的 RNN 去表达 Attention，有一定的局限性。 RNN 的计算隐状态 hidden 都是不变的，即每个信息（片段）仅仅只有一个维度，只有一个值。
所以 Attention 机制 将 hidden 分拆成 key 和 value，且 query 循环和所有的 key 和 value 计算后才得到 Score。

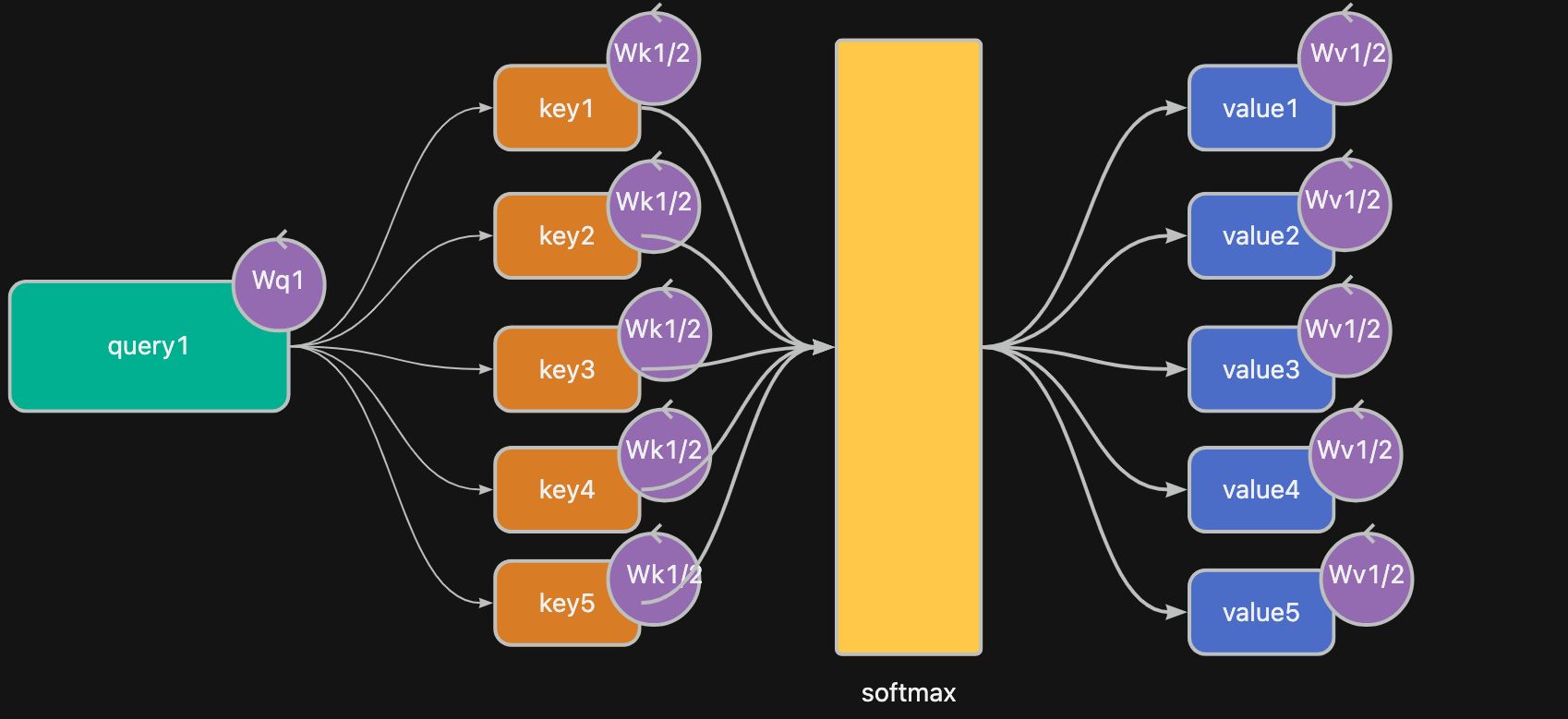
上图简化出来的公式就是 Attention Score = $Attention(QW^Q,KW^K,VW^V)$ ，就是 注意力评分公式 了。

这种把 hidden 拆分成 key 和 value，并且结合 query 计算就是 QKV 机制（ query key value 机制）。

多头注意力机制

Multiple Head Attention

从上述的 QKV 机制 知道，query 就是根据兴趣点，触发对片段计算评分。
如果仅仅是一个 query，其实和单一使用 RNN hidden 是没有区别的；但是如果增加多几个 query，就可以对信息进行不同维度的分层，也就是多头的意思。

🔥 多头注意力机制，就是字如其名，多个 head，多个 query；一个 head 就是一个 query。

比如，“姚明为什么这么高”，“他三角函数不懂” 这两个 query 都同时对原信息进行统计评分，就可以得到不同 segment 对应的 Attention Score。

🔥 有点像是 CNN 的卷积核，可以抽取不同的特征维度。

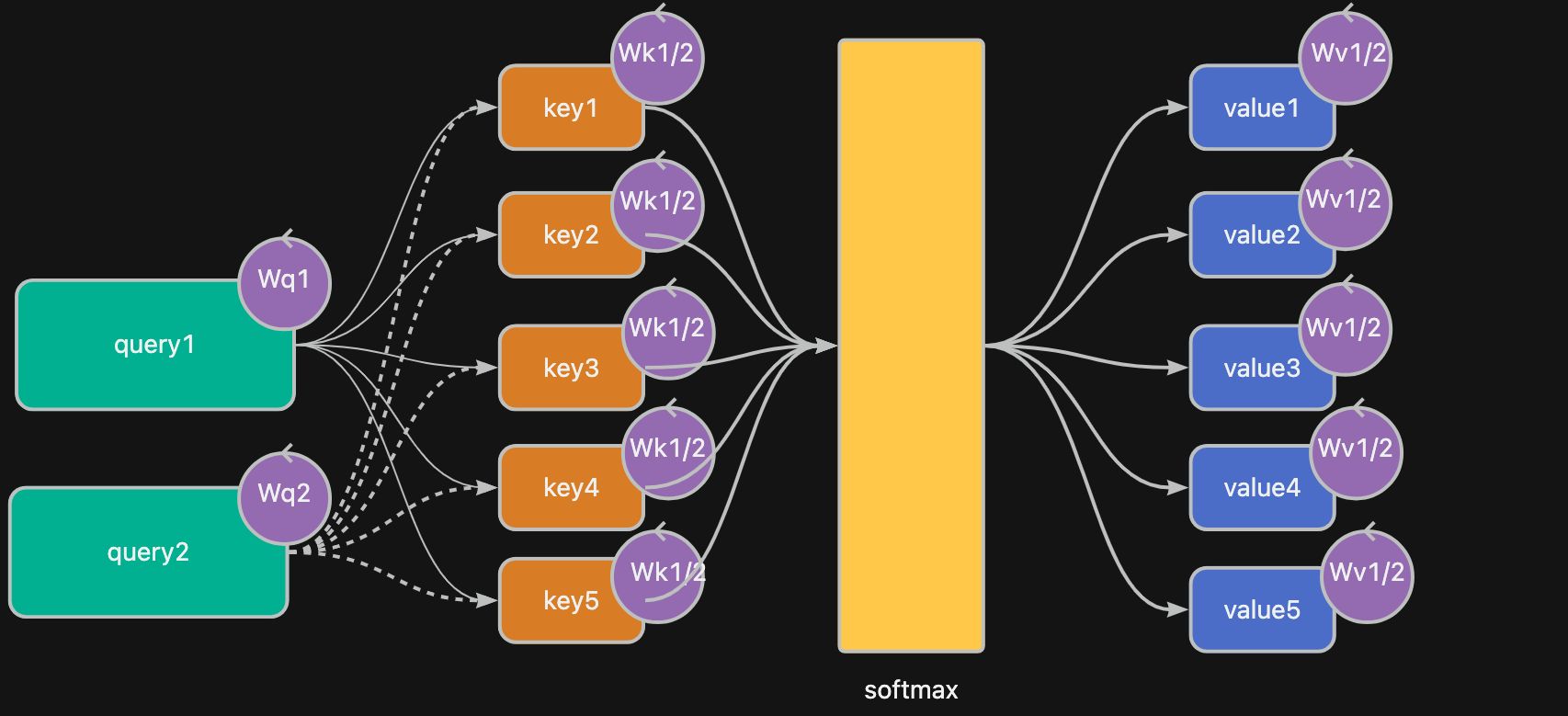
query, key, value 因为不同的 head 都带有自己的（$W^Q W^K W^V$）矩阵进行学习，这样就能够带来更加多的学习性。

自注意力机制

Self Attention

有时候，一句话中，已经蕴含了逻辑。比如上面的“姚明描述”，就算没有提问，都可以从自身的句子中建立了关联。

比如，“他从小的数学成绩并不好” seg2 和 “经常旷课” seg3，他们两个片段就有非常强的相关性，他们 Attention Score 的得分就高；同理“经常旷课” seg3，“他爱吃苹果” seg4，他们的得分就不高。

🔥 所以当 Query Key Value 都是自己的，就是 自注意力机制，对自己的信息片段建立 Attention Score。

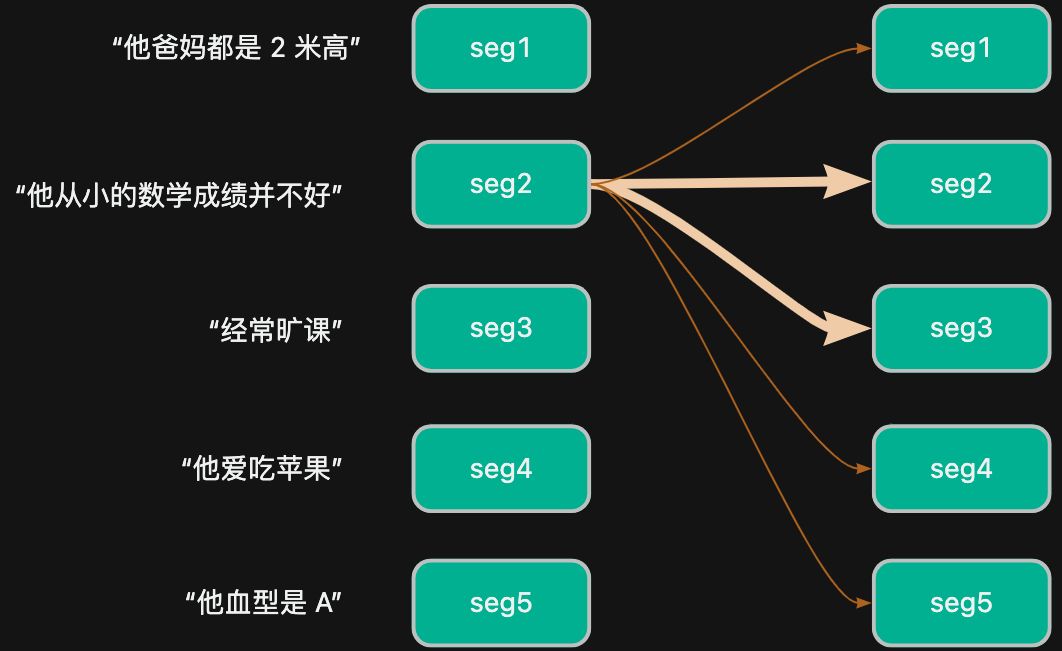
上图可以知道，越粗的线，就是他们的 attention score 更加的高分；且这是自身片段和片段之间的评分。就是自注意力机制的体现。

注意力得分代码部分

Attention Score，到底他们是如何计算的呢？
下面是简易自注意力得分的代码片段。里面已经包含了 QKV 机制，多头注意力机制，和 自注意力机制。

# [0]
query_f = nn.Linear(d_model, d_model)
key_f = nn.Linear(d_model, d_model)
value_f = nn.Linear(d_model, d_model)
fc = nn.Linear(d_model, d_model)
# [3]
def forward(self, query, key, value, mask=None):
    batch_size = query.size(0)

    def transform(x):
        return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
    # [1] 对 query，key，value 进行全链接的转换
    query = transform(query_f(query))
    key = transform(key_f(key))
    value = transform(value_f(value))
    # [2] 封装的方法
    attn_output, attn = ScaledDotProductAttention(self.d_k)(query, key, value, mask)

_代码解析_：

[0] query_f，key_f， value_f 定义全链接网络，用于学习的参数
[1] query，key，value 进行全链接的转换，这里有参数的学习
[2] 封装的方法，可以计算出最后的 Attention Sore，里面已经包含点积/softmax 等计算
[3] 如果 query, key, value 都是同一个变量的时候，那么就是一个 多头的自注意力机制 的计算公式

多头自注意力机制的数学表达式：
$head_i=Attention(QW_i^Q,KW_i^K,VW_i^V)$ （ $W_i^Q W_i^K W_i^V$ 都是不同的全链接网络）

例子说明

可运行的 ipynb 文件链接。
任务：输入数据，计算数据之间的注意力分数，并且可以视觉化数据之间的关注度。

代码解析

input_seq = torch.tensor([
    [1.0, 0.0, 1.0, 0.0],  # Token 1
    [0.0, 1.0, 0.0, 1.0],  # Token 2
    [1.0, 1.0, 0.0, 0.0],  # Token 3
    [0.0, 0.0, 1.0, 1.0],  # Token 4
    [1.0, 0.5, 0.5, 0.0]   # Token 5
], dtype=torch.float32)

# Dimensions
d_k = input_seq.shape[1]  # Embedding dimension (4 in this case)

# Query, Key, and Value are all set to the input sequence (self-attention)
query = input_seq
key = input_seq
value = input_seq

# Calculate attention scores (scaled dot-product)
# [1]
scores = torch.matmul(query, key.transpose(-2, -1)) / torch.sqrt(torch.tensor(d_k))
print("Attention scores:\n", scores)
# Apply softmax to get attention weights
# [2]
attention_weights = F.softmax(scores, dim=-1)
print("Attention scores afert softmax:\n", attention_weights)

# Calculate the output as a weighted sum of the values
# [3]
output = torch.matmul(attention_weights, value)

print("Attention Weights:\n", attention_weights)

[1] 简单使用对 query key 进行点积来计算分数

这里使用了简化版本，没有 $W^q$ $W^k$ 的矩阵学习
[2] softmax score，全部值归一到 (0,1) 的值中
[3] score 和 value 相乘，得到最后的 weights，就是最后的结果

这里使用了简化版本，没有 $W^v$ 的矩阵学习

运行结果

'''
Attention scores:
 tensor([[1.0000, 0.0000, 0.5000, 0.5000, 0.7500],
        [0.0000, 1.0000, 0.5000, 0.5000, 0.2500],
        [0.5000, 0.5000, 1.0000, 0.0000, 0.7500],
        [0.5000, 0.5000, 0.0000, 1.0000, 0.2500],
        [0.7500, 0.2500, 0.7500, 0.2500, 0.7500]])
Attention scores afert softmax:
 tensor([[0.2976, 0.1095, 0.1805, 0.1805, 0.2318],
        [0.1205, 0.3275, 0.1986, 0.1986, 0.1547],
        [0.1805, 0.1805, 0.2976, 0.1095, 0.2318],
        [0.1986, 0.1986, 0.1205, 0.3275, 0.1547],
        [0.2374, 0.1440, 0.2374, 0.1440, 0.2374]])
Attention Weights:
 tensor([[0.2976, 0.1095, 0.1805, 0.1805, 0.2318],
        [0.1205, 0.3275, 0.1986, 0.1986, 0.1547],
        [0.1805, 0.1805, 0.2976, 0.1095, 0.2318],
        [0.1986, 0.1986, 0.1205, 0.3275, 0.1547],
        [0.2374, 0.1440, 0.2374, 0.1440, 0.2374]])
'''

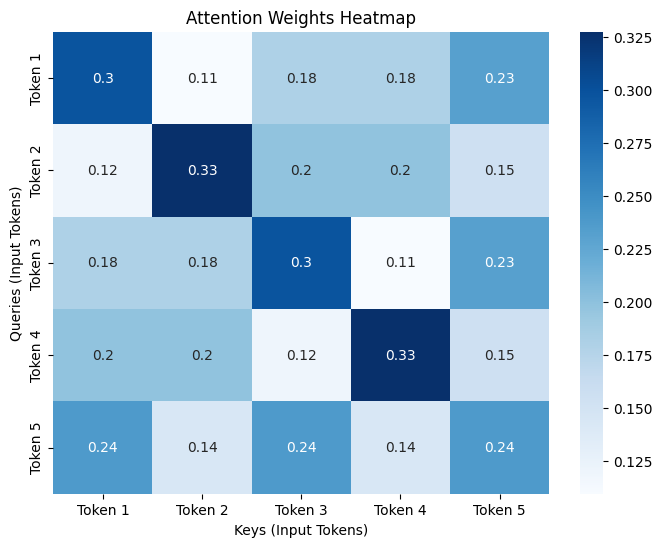
从图上可以看到，注意力的热图，表示每个 token 之间的注意力的关系。 Y 轴是 Query Token，X 轴是 Key Token。图中每一行中越深色的方块，就代表 Query 在这行中的 Key 的得分最高。
比如，第一行，query1 对 key1（自己）的颜色最深，说明每个 Token 都应该与自己的关联度高；第 5 行，query5 对 key1，key3，key5 的得分一样且颜色最深，说明 query5 的关联与 key1，key3，key5 相一样。